1、激活函数含义

1.1、什么是激活函数？

激活函数是人为增加的一种功能，这种功能也被称为“传递函数”，目的是为了增加函数的“非线性能力”。

1.2、为什么要用激活函数？

如果不用激活函数，那么无论神经网络是多少层，输出都是一个“线性变化”。这种情况就是原始的“感知机”。 如果使用了激活函数，神经元就会逼近任何的“非线性函数”。这样模型有更多的拟合能力。

下面的图表示线性分割的图像：

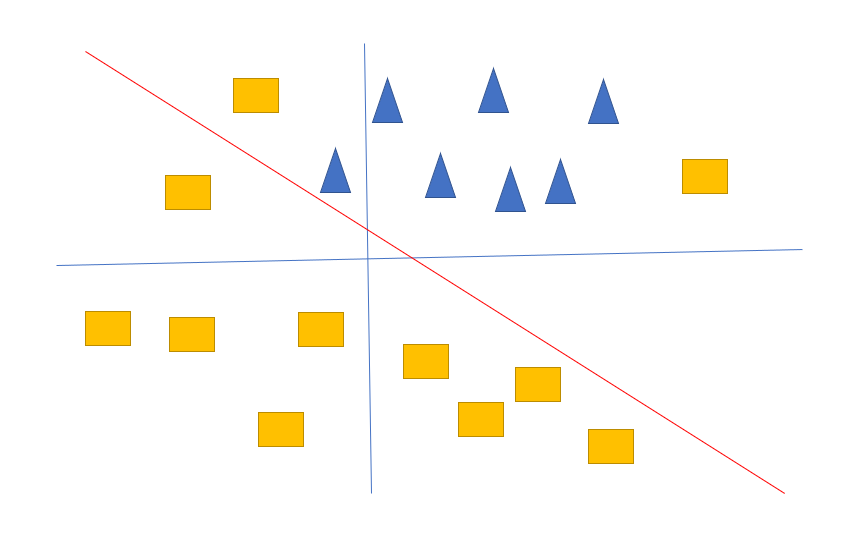
实际上我们其实想要的是这样的分割线

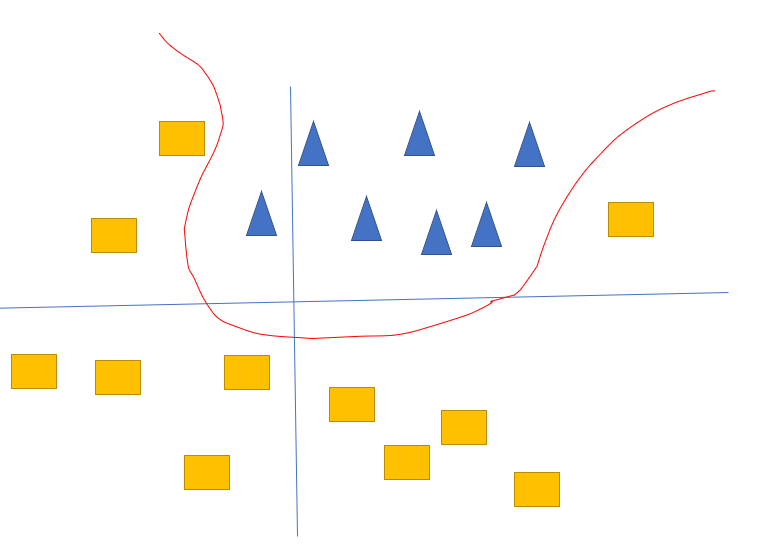
【注意】如果我们不用激活函数，就单纯的想增加隐藏层，能否达到类似激活函数的效果？ 答案是：否

因为增加层数，就会单纯的增加Wx+b的个数，线性函数有一个特性：两个线性相加还是等于线性函数。 所以无论多少个Wx+b都可以合并同类型。变成一个更大的W'x+b'这样的形式

1.3、什么是线性函数

线性函数的解释：只要满足线性关系的都叫线性函数 满足两个关系：假如有这样的关系： $$ f(x) = y $$

$$ 1、f(x_i)=y_i \ 且 \ f(x_1+x_2)=y_1+y_2 $$

$$ 2、f(K*x)=K*y \ 且 \ K是一个常数 $$

满足这样的关系的函数，就叫线性函数。

2、激活函数的种类

2.1、单变量输入激活函数

2.1.1、恒等函数

定义：设M为一集合，于M上的恒等函数f被定义于一具有定义域和陪域M的函数，其对任一M内的元素x，会有f(x)=x的关系。

图像：

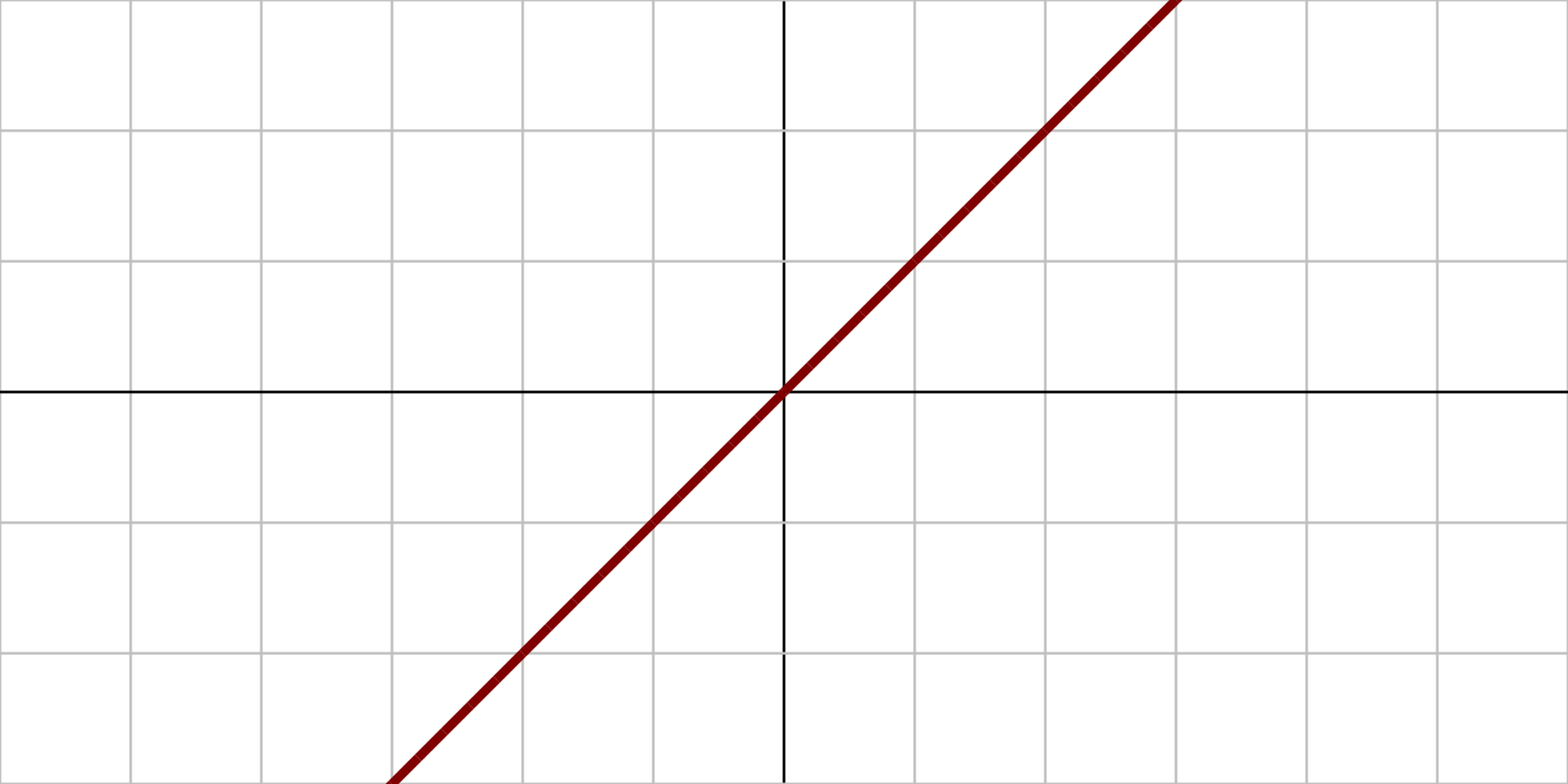
原函数： $$ f(x) =x $$ 导函数： $$ f'(x)=1 $$

2.1.2、单位阶跃函数

定义：又称赫维赛德阶跃函数，通常用 H 或 θ 表记，有时也会用 u、1 或 𝟙 表记，是一个由奥利弗·亥维赛提出的阶跃函数，参数为负时值为0，参数为正时值为1。

图像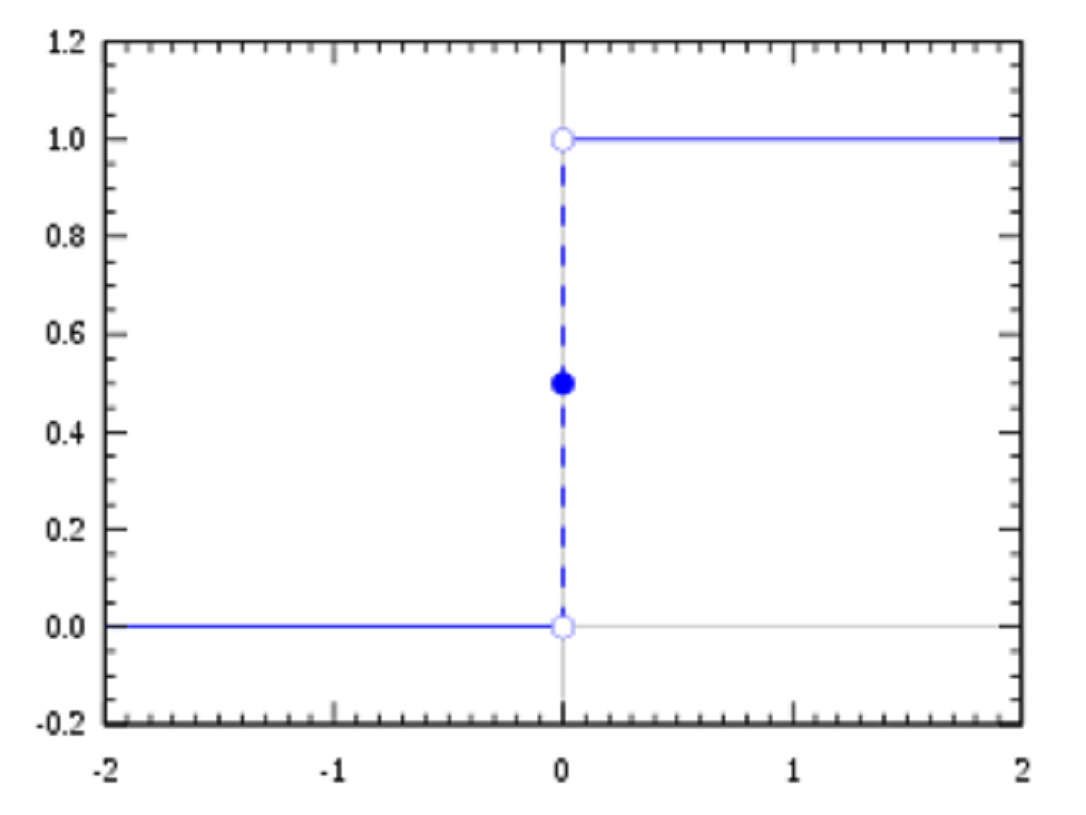： 原函数：

$$ f(x)=\begin{Bmatrix} 0 \ x<0 \\ 1 \ x\geqslant 0 \\ \end{Bmatrix} $$

导函数：

$$ f'(x)=\begin{Bmatrix} 0 \ x\neq 0 \\ 无 \ x=0 \\ \end{Bmatrix} $$

2.1.3、逻辑函数

定义： 一种常见的S型函数，其曲线逻辑斯谛曲线是一种S型曲线

图像：

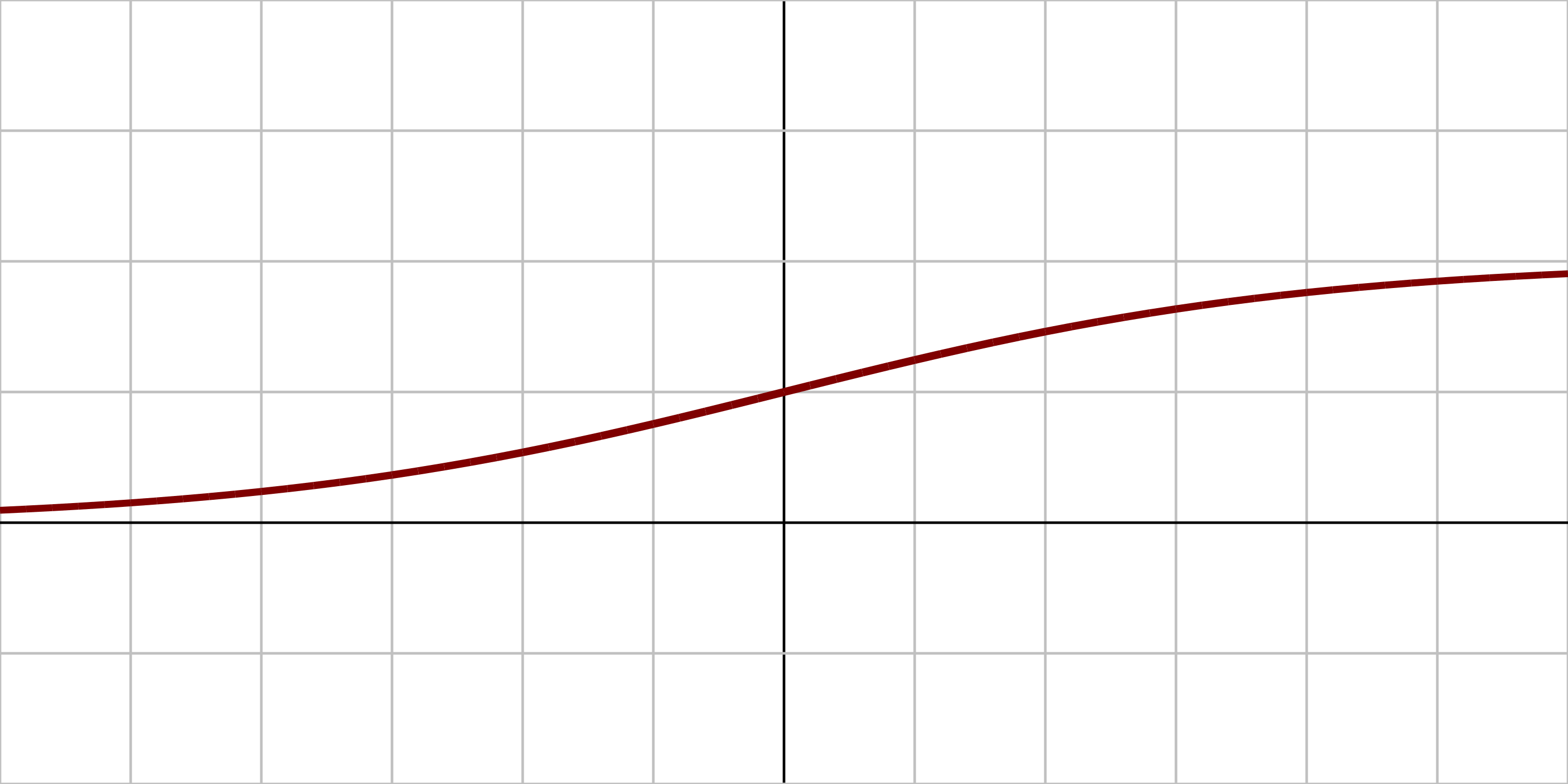
原函数： $$ f(x)=\sigma(x) + \frac{1}{1+e^{-x}} $$ 导数 $$ f'(x) = f(x)(1-f(x)) $$

2.1.4、双曲正切函数

定义： 双曲正弦一般计为 sinh,其在复变分析中定义为: $$ {\displaystyle \sinh :z\mapsto {\frac {\mathrm {e} ^{z}-\mathrm {e} ^{-z}}{2}}} $$

图像：

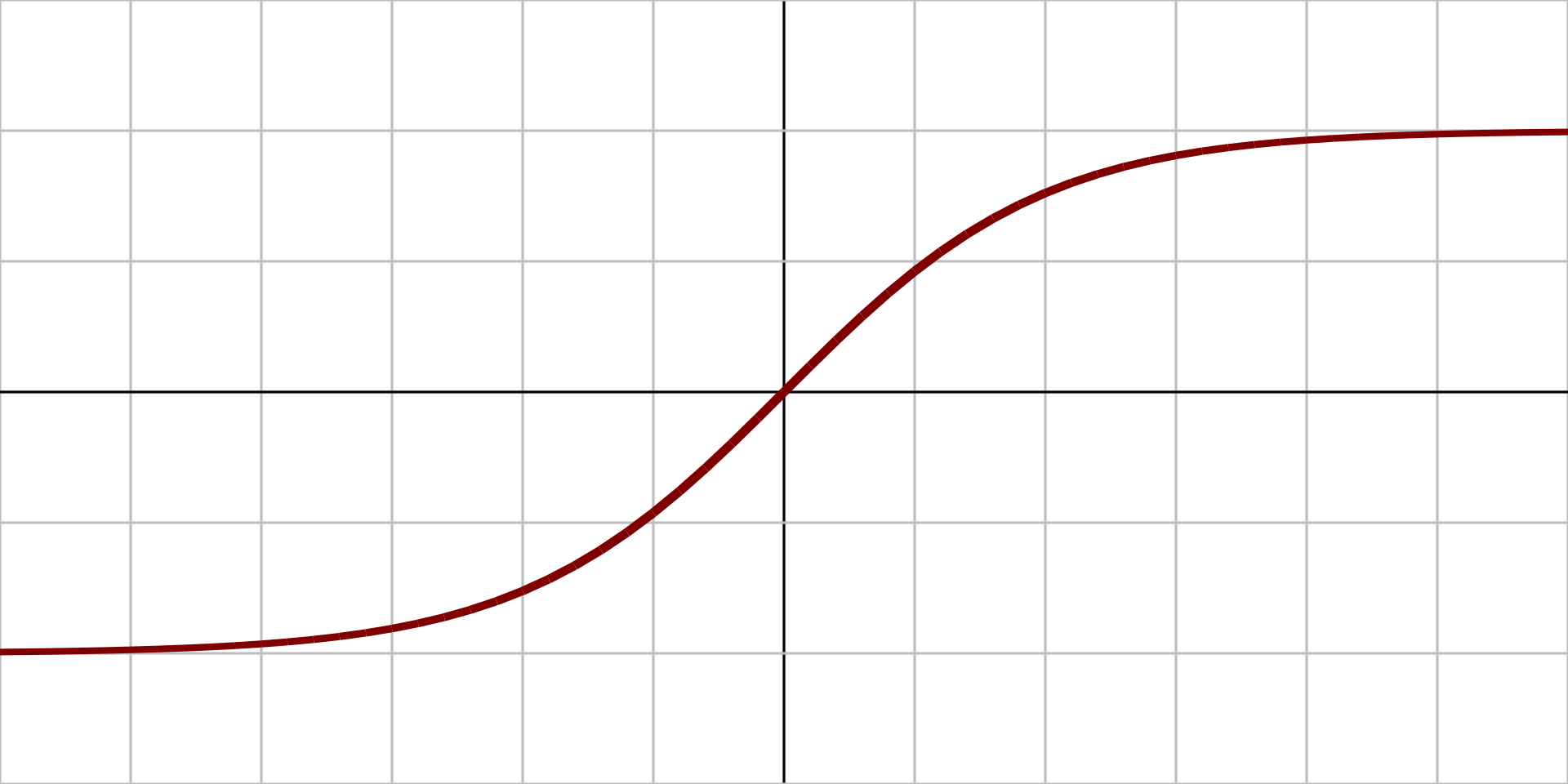
原函数： $$ {\displaystyle f(x)=\tanh(x)={\frac {(e^{x}-e^{-x})}{(e^{x}+e^{-x})}}} $$

导数： $$ {\displaystyle f'(x)=1-f(x)^{2}} $$

2.1.5、反正切函数

定义： 反正切是一种反三角函数，是利用已知直角三角形的对边和邻边这两条直角边的比值求出其夹角大小的函数，是高等数学中的一种基本特殊函数。 在三角学中，反正切被定义为一个角度，也就是正切值的反函数，由于正切函数在实数上不具有一一对应的关系，所以不存在反函数， 但我们可以限制其定义域，因此，反正切是单射和满射也是可逆的，但不同于反正弦和反余弦，由于限制正切函数的定义域在 $$ {\displaystyle [-{\frac {\pi }{2}},{\frac {\pi }{2}}]}[-{\frac {\pi }{2}},{\frac {\pi }{2}}] $$ 时，其值域是全体实数，因此可得到的反函数定义域也是全体实数，而不必再进一步去限制定义域。

图像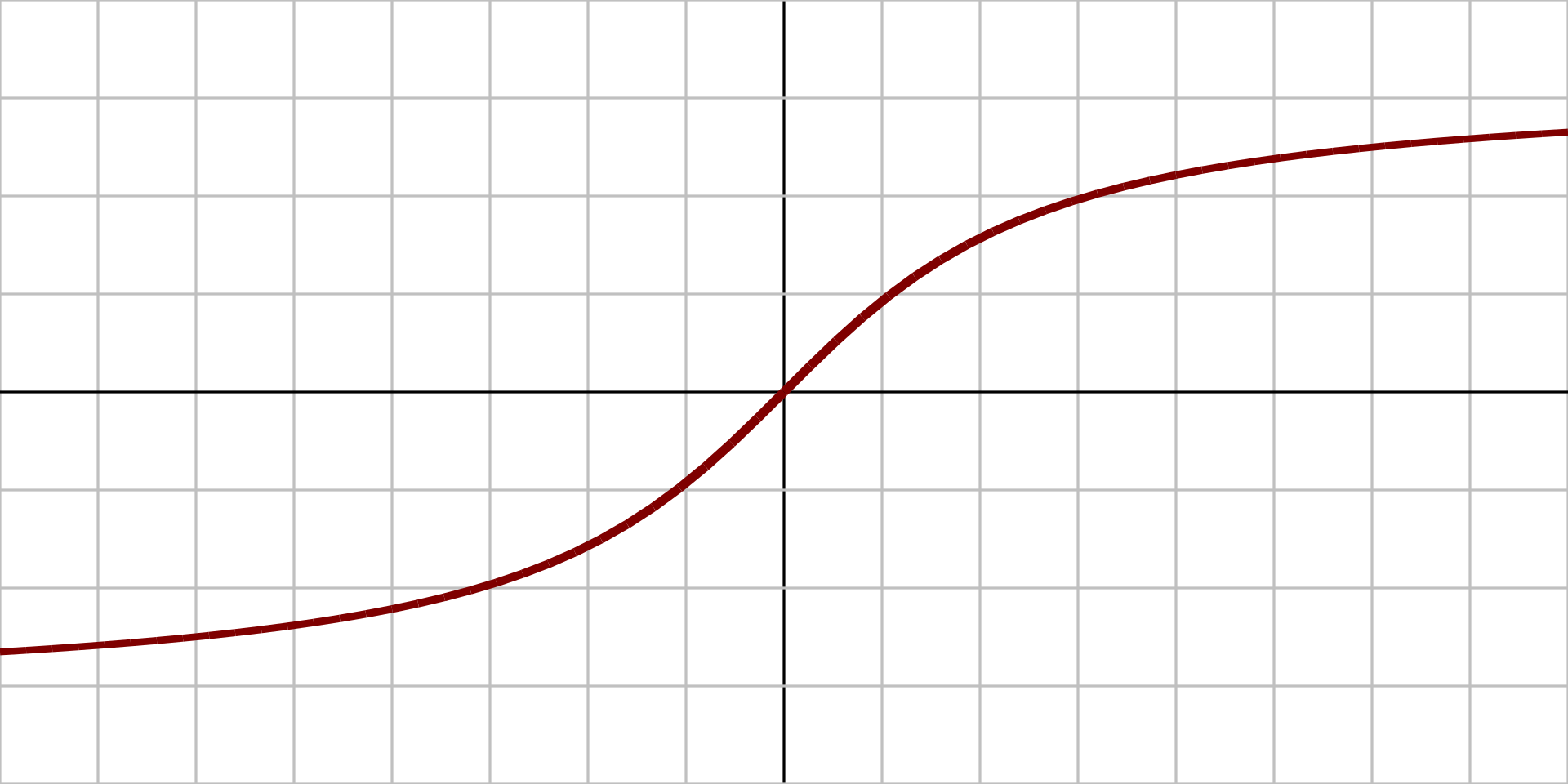： 原函数： $$ {\displaystyle f(x)=\tan ^{-1}(x)} $$ 导数： $$ {\displaystyle f'(x)={\frac {1}{x^{2}+1}}} $$

2.1.6、Softsign函数

图像：

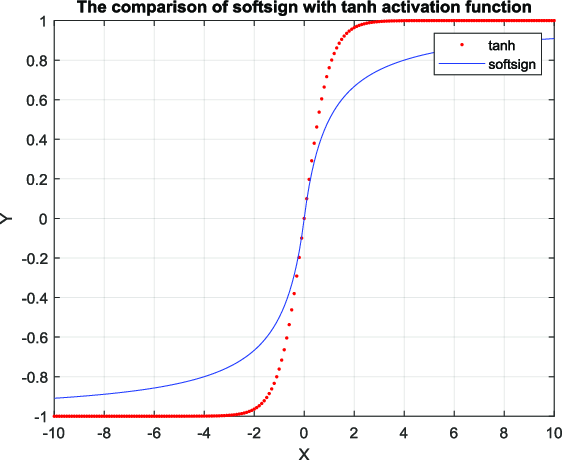
原函数： $$ {\displaystyle f(x)={\frac {x}{1+|x|}}} $$

导数： $$ {\displaystyle f'(x)={\frac {1}{(1+|x|)^{2}}}} $$

2.1.7、反平方根函数 (ISRU)

图像：

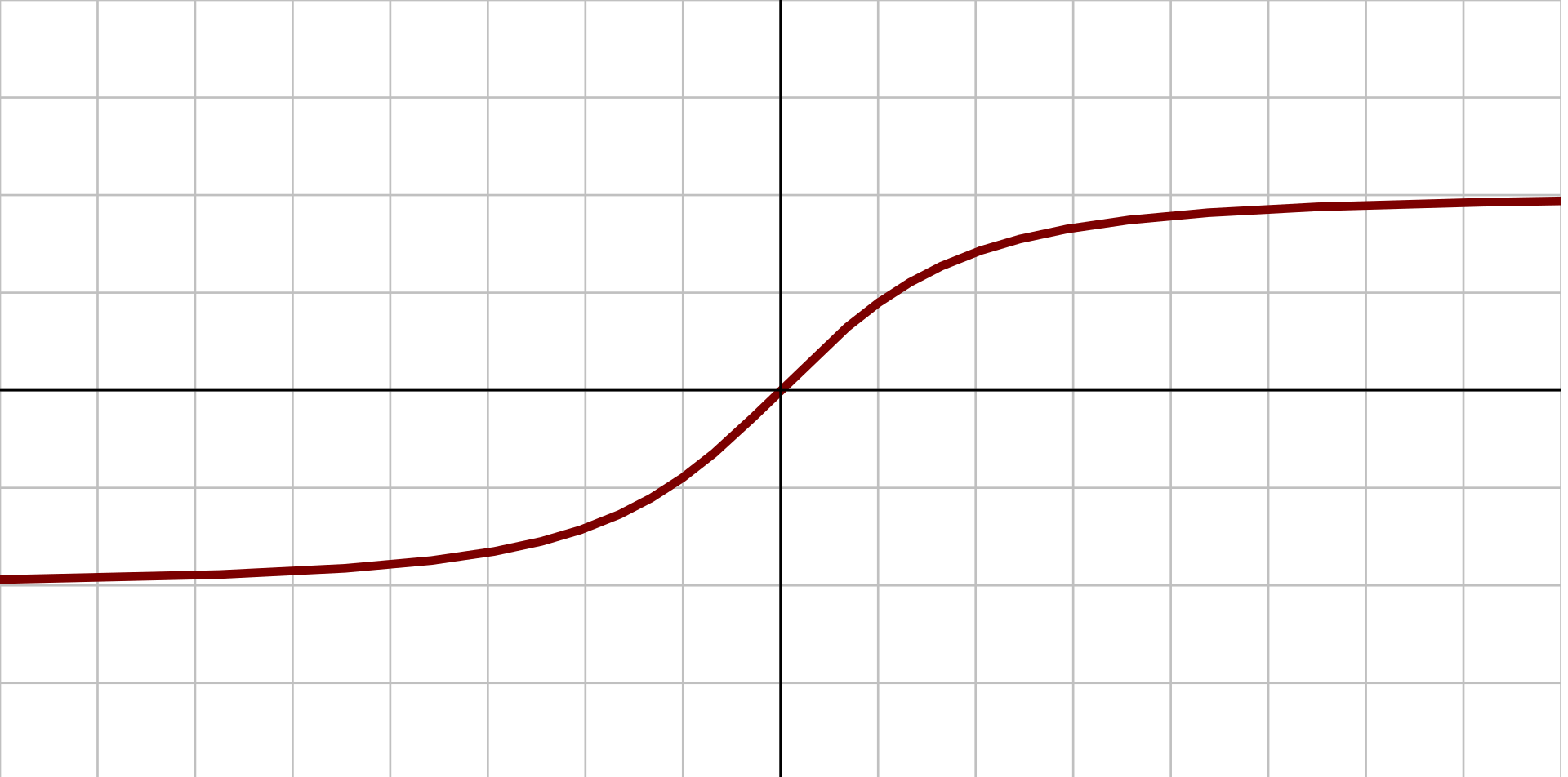
原函数： $$ {\displaystyle f(x)={\frac {x}{\sqrt {1+\alpha x^{2}}}}} $$

导数： $$ {\displaystyle f'(x)=\left({\frac {1}{\sqrt {1+\alpha x^{2}}}}\right)^{3}} $$

2.1.8、线性整流函数 (ReLU)

图像：

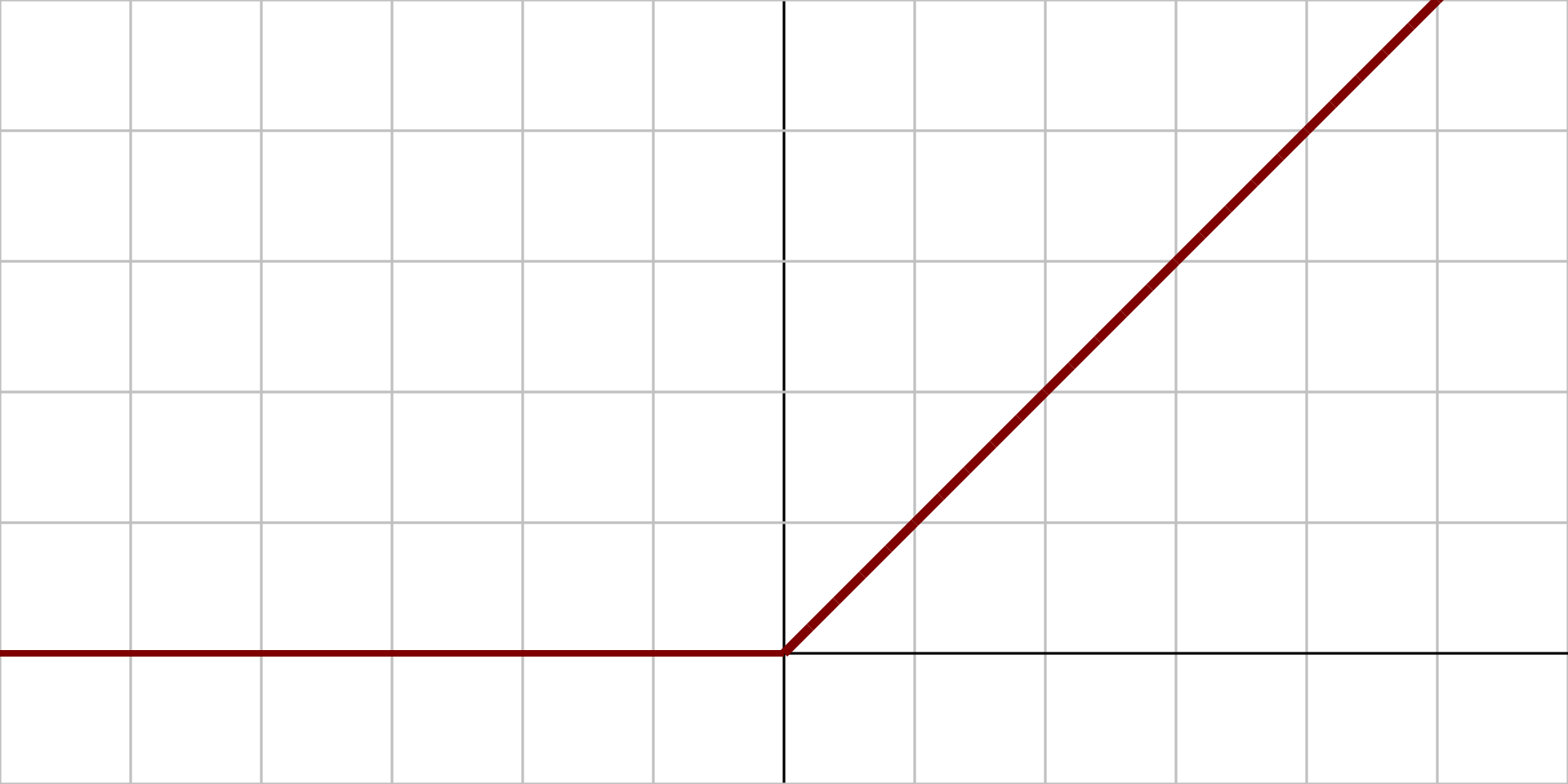
原函数： $$ {\displaystyle f(x)={\begin{cases}0&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}} $$

导数： $$ {\displaystyle f'(x)={\begin{cases}0&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}} $$

2.1.9、带泄露线性整流函数 (Leaky ReLU)

图像：

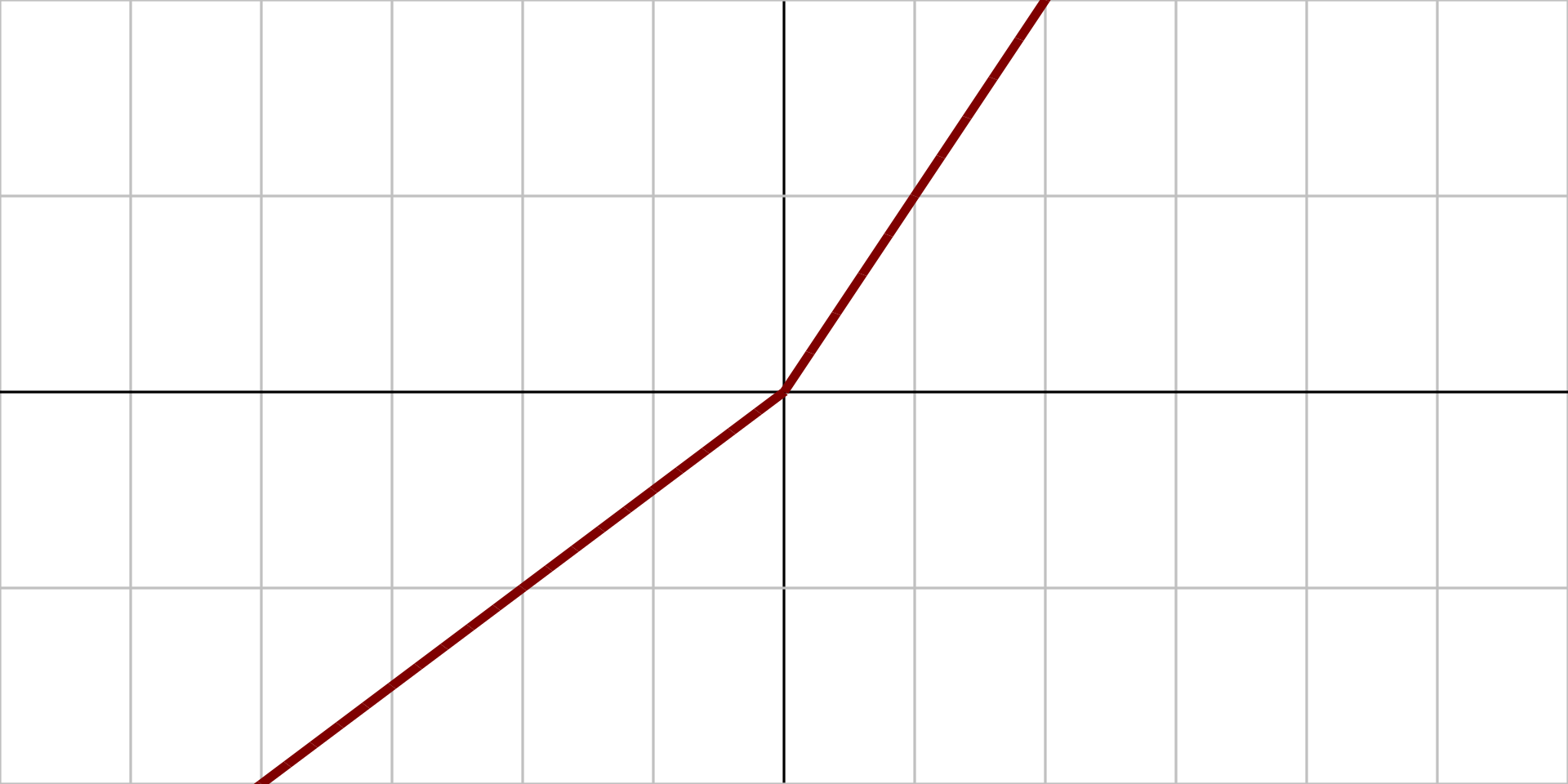
原函数： $$ {\displaystyle f(x)={\begin{cases}0.01x&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}} $$

导数： $$ {\displaystyle f'(x)={\begin{cases}0.01&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}} $$

2.1.10、参数化线性整流函数 (PReLU)

图像：

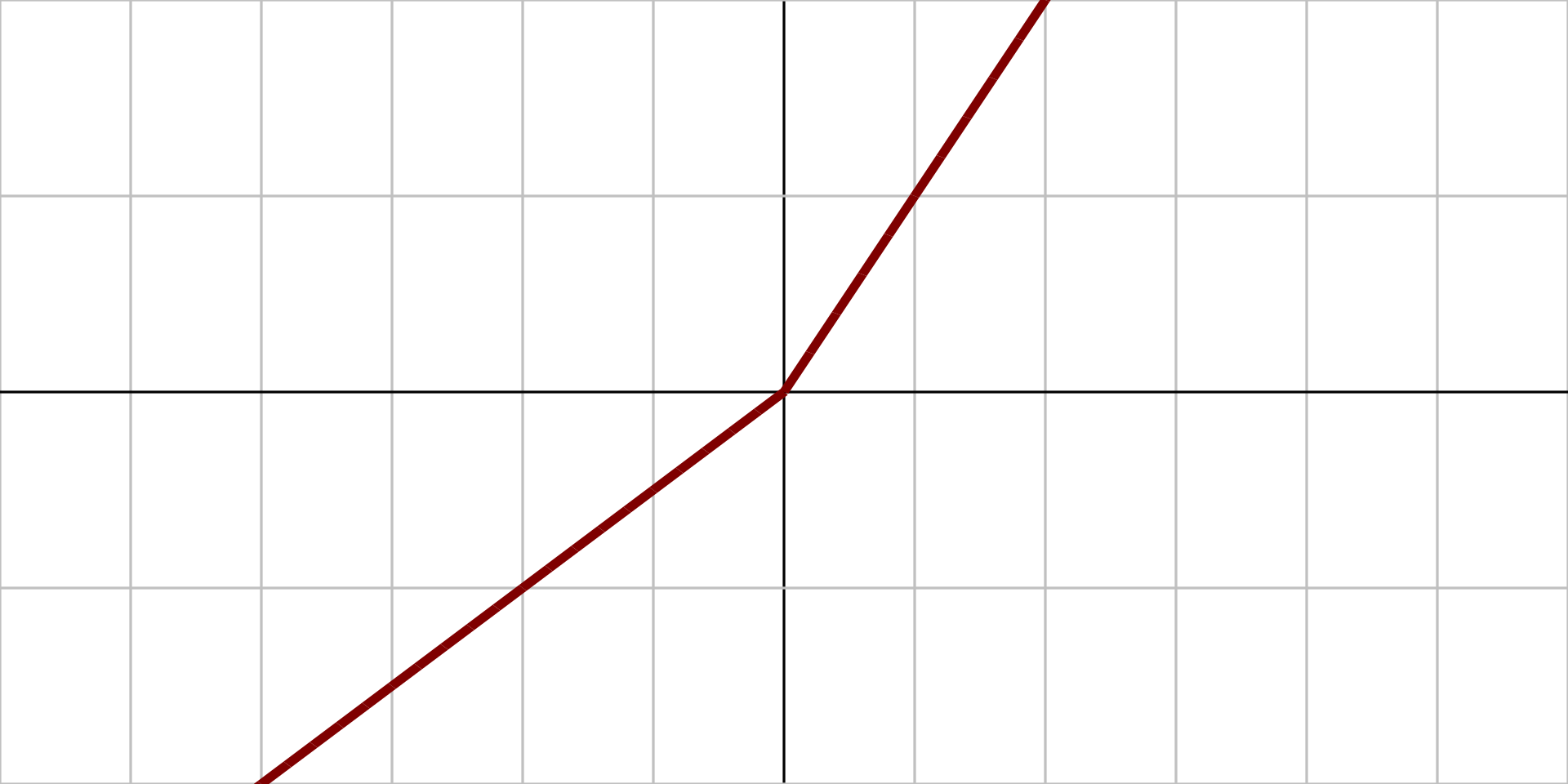
原函数： $$ {\displaystyle f(\alpha ,x)={\begin{cases}\alpha x&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}} $$

导数： $$ {\displaystyle f'(\alpha ,x)={\begin{cases}\alpha &{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}} $$

2.1.11、指数线性函数 (ELU)

图像：

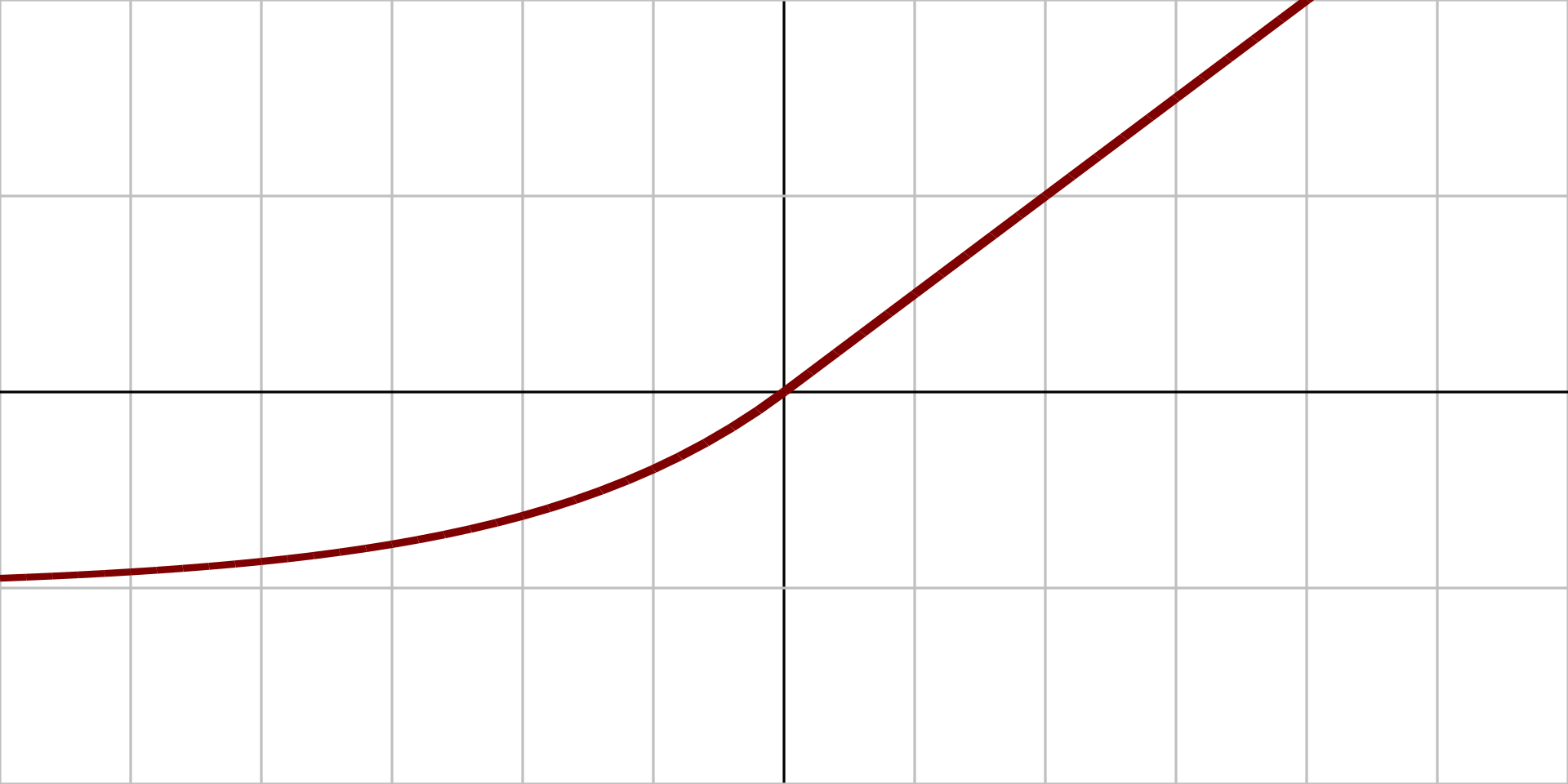
原函数： $$ {\displaystyle f(\alpha ,x)={\begin{cases}\alpha (e^{x}-1)&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}} $$

导数： $$ {\displaystyle f'(\alpha ,x)={\begin{cases}f(\alpha ,x)+\alpha &{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}} $$

2.2、多变量输入激活函数

2.2.1、Softmax函数

原函数： $$ f_{i}({\vec{x}})=\frac{e^{x_{i}}}{\sum_{j=1}^{J}e^{x_{j}}} \ 且 \ i = 1, …, J $$

导数： $$ {\displaystyle {\frac{\partial f_{i}({\vec{x}})}{\partial x_{j}}}=f_{i}({\vec{x}})(\delta_{ij}-f_{j}({\vec{x}}))} $$

2.2.2、Maxout函数

原函数： $$ {\displaystyle f({\vec{x}})=\max_{i}x_{i}} $$

导数： $$ {\displaystyle {\frac{\partial f}{\partial x_{j}}}={\begin{cases}1&{\text{for }}j={\underset{i}{\operatorname{argmax}}},x_{i}\\0&{\text{for }}j\neq{\underset{i}{\operatorname{argmax}}},x_ {i}\end{cases}}} $$

3、选择激活函数

3.1、sigmoid

Sigmoid函数曾被广泛应用，但由于其自身的一些缺陷，现在已经很少用了。现在已经不推荐使用了

3.2、Tanh

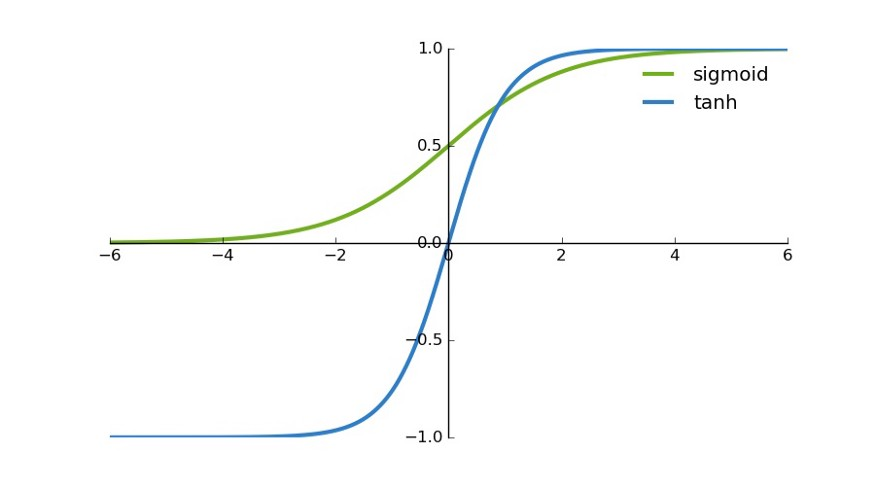tanh函数与Sigmoid函数非常相似。它实际上只是Sigmoid函数的一个放大版本。 它基本上解决了所有值符号相同的问题，而其他属性都与sigmoid函数相同。 函数具有连续性和可微性。你可以看到函数是非线性的，所以我们可以很容易地将误差进行反向传播。 所以可以使用tanh来替代Sigmoid函数。 与Sigmoid函数相比，tanh函数的梯度更陡。 使用sigmoid函数还是tanh函数取决于问题陈述中对梯度的要求。 但是tanh函数出现了Sigmoid函数类似的问题，梯度渐趋平坦，并且值非常低。

3.3、ReLU

ReLU是近几年非常受欢迎的激活函数 ReLU是如今设计神经网络时使用最广泛的激活函数。首先，ReLU函数是非线性的，这意味着我们可以很容易地反向传播误差，并激活多个神经元。 ReLU函数优于其他激活函数的一大优点是它不会同时激活所有的神经元。这是什么意思?如果输入值是负的，ReLU函数会转换为0， 而神经元不被激活。这意味着，在一段时间内，只有少量的神经元被激活，神经网络的这种稀疏性使其变得高效且易于计算。 ReLU函数也存在着梯度为零的问题。看上图，x＜0时，梯度是零，这意味着在反向传播过程中，权重没有得到更新。这就会产生死神经元，而这些神经元永远不会被激活。

3.3.1、Leaky ReLU

Leaky ReLU函数只是一个ReLU函数的改良版本。我们看到，在ReLU函数中，x < 0时梯度为0，这使得该区域的神经元死亡。 为了解决这个问题， Leaky ReLU出现了。这是它的定义： 替换水平线的主要优点是去除零梯度。在这种情况下，梯度是非零的，所以该区域的神经元不会成为死神经元。 与Leaky ReLU函数类似的，还有PReLU函数，它的定义与Leaky ReLU相似。 然而， 在PReLU函数中，a也是可训练的函数。神经网络还会学习a的价值，以获得更快更好的收敛。 当Leaky ReLU函数仍然无法解决死神经元问题并且相关信息没有成功传递到下一层时，可以考虑使用PReLU函数。

3.4、Softmax

softmax函数也是一种sigmoid函数，但它在处理分类问题时很方便。sigmoid函数只能处理两个类。当我们想要处理多个类时，该怎么办呢？只对单类进行“是”或“不是”的分类方式将不会有任何帮助。 softmax函数将压缩每个类在0到1之间，并除以输出总和。它实际上可以表示某个类的输入概率。 比如，我们输入[1.2,0.9,0.75]，当应用softmax函数时，得到[0.42,0.31,0.27]。现在可以用这些值来表示每个类的概率。 softmax函数最好在分类器的输出层使用。

3.2、结果

• 用于分类器时，Sigmoid函数及其组合通常效果更好。
• 由于梯度消失问题，有时要避免使用sigmoid和tanh函数。
• ReLU函数是一个通用的激活函数，目前在大多数情况下使用。
• 如果神经网络中出现死神经元，那么PReLU函数就是最好的选择。
• 请记住，ReLU函数只能在隐藏层中使用。

3.3、最新的激活函数

Switch-B(searching for activation functions)

Swish是Google在2017年10月16号提出的一种新型激活函数,其原始公式为: $$ f(x)=x * Sigmod(x) $$ 变形Swish-B激活函数的公式则为 $$ f(x)=x * Sigmod(b * x) $$ 其拥有不饱和,光滑,非单调性的特征,而Google在论文中的多项测试表明Swish以及Swish-B激活函数的性能即佳, 在不同的数据集上都表现出了要优于当前最佳激活函数的性能.